Demension Reduction
우리가 세상에서 얻는 데이터들은 수 많은 component들로 이루어진 vector로 나타낼 수 있다. 고차원으로 이루어진 데이터를 처리하는데에는 많은 자원과 시간이 필요하다. 그러므로 우리는 어떻게 고차원의 데이터를 저차원의 데이터로 변환할 수 있는지에 중점을 두고 살펴볼 것이다.
Feature Selection
- 고차원의 데이터 중에서 데이터를 표현할 때 중요한 feature를 뽑아 그 값을 그대로 사용하는 방법
Feature Projection
- 고차원의 데이터를 어떠한 수학적 방법을 통하여 다른 차원으로 transform 시키는 방법
- demension reduction의 대표적인 방법

Principal Components Analysis(PCA)
PCA를 설명하기 위해서 세 가지의 큰 범주로 나누었다.
1. X --> Y ( PX = Y )
- Linear Data Projection
- X를 선형변환(P)을 통해서 Y로 만들어준다.
- 어떠한 선형변환(P)인지는 아래에서 설명한다.
2. Basis Change
- 데이터를 더 잘 표현할 수 있는 축으로 바꾸어준다.
- 간단히 설명하자면 아래와 같이 설명할 수 있다.

지금 상황에서는 빨간색 공의 움직임을 관찰하기 위해 카메라 A, B, C 총 3대가 공을 촬영하고 있다.
하지만 잘 생각해보면 빨간색 공은 xy평면에서 x축의 변화만 있을 것이다. 그러므로 카메라 3대가 아닌 x축에서 찍는 카메라 1대만 있다면 빨간색 공의 움직임을 정확히 관찰할 수 있을 것이다.
3. Minimize Redundancy
- 중복된 데이터를 최대한 없앤다.
어떠한 2개의 데이터의 A, B가 있다고 가정, A와 B 데이터의 중복성을 알아내기 위한 방법 중 하나는 2개의 데이터의 상관관계를 알아보는 것이다. A의 값이 증가할 때 B의 값 또한 증가하고, A의 값이 감소할 때 B의 값 또한 감소한다면 2개의 데이터는 관련이 있는 데이터라고 생각할 수 있다. 반대의 경우에는 2개의 데이터는 관련이 없는 데이터라고 생각할 수 있다.
그렇다면 2개의 데이터의 상관관계를 어떻게 알 수 있을까? 바로 고등학생 시절에 배운 확률과 통계 파트에 나오는 공분산을 이용하는 것이다. 공분산은 2개의 확률변수의 상관정도를 나타내는 값이다.

A와 B의 데이터가 관련이 없다면 값이 0이 될 것이고 그와 반대로 관련이 있다면 0이 아닌값이 될 것이다.
- 공분산 행렬
데이터 x = (x1, x2, x3

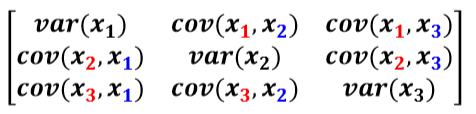
정리
다시 1번으로 돌아가 P에 대해서 알아볼 시간이 된 것 같다.
PX = Y에서 Y가 되어야 할 조건을 먼저 생각해본다면 Y의 데이터들은 서로 상관관계가 없어야 할 것이다.
즉 Y의 공분산 행렬은 대각선 부분을 제외한 데이터가 0인 행렬(diagonal matrix)이 되어야한다. 이 행렬을 가중치에 따라 정렬한 후 가중치가 낮다고 생각하는 데이터를 제거하면 행렬 P가 된다.


관련 패키지
from sklearn.decomposition import PCA
'2020_1학기_알고리즘응용' 카테고리의 다른 글
| Week08 Viterbi Search (0) | 2020.06.07 |
|---|---|
| Week07 Representation Learning and Deep Learning (0) | 2020.06.07 |
| Week04 Clustering (0) | 2020.06.05 |
| Week03 Distance metric (0) | 2020.06.02 |
| Week02 Tools for Data Understanding (0) | 2020.06.02 |




댓글